- Переместительное свойство сложения.
- Сочетательное свойство сложения.
- Сложение с числом 0.
- Знать свойства сложения.
- Уметь проводить вычисления «удобным способом».
- Расположите числа в порядке возрастания а) 385748; б) 339482; в) 304958;
г) 4952004; д) 39482. - Назовите числа, между которыми заключено число а) 35492; б) 1909; в) 49850.
В первом классе, чтобы к 7 прибавить 2, нужно было к числу 7 прибавить сначала 1, потом к полученной сумме прибавить еще 1.
Получаем 7+2=7+1+1= 8+1=9.
Интересно, почему в начальной школе нам так непросто было находить сумму чисел, а теперь мы все вычисления с однозначными числами производим «в уме», пример 4+9=13, 8+7=15? Дело в том, что при многократном повторении мы уже знаем наизусть таблицу сложения однозначных чисел. Именно поэтому считать многозначные числа в столбик удобнее, так как при поразрядном сложении мы имеем дело только с этой группой чисел.
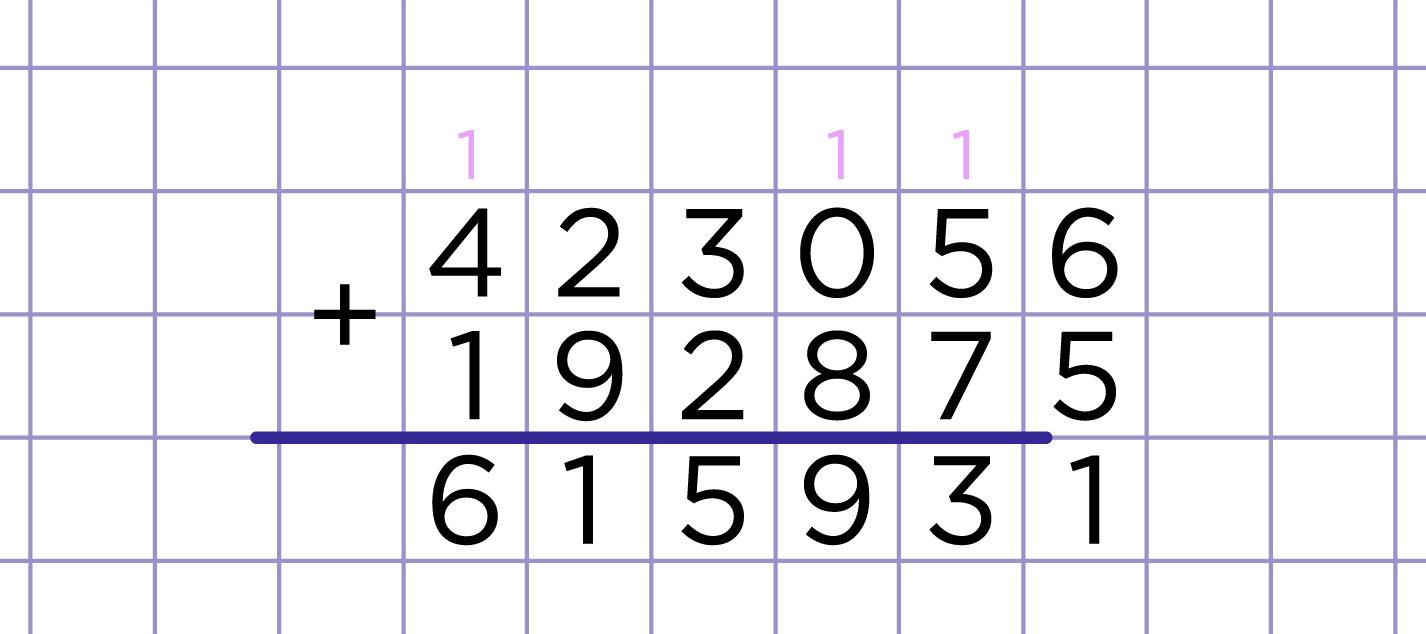 Рис. 1. Пример сложения в столбик
Рис. 1. Пример сложения в столбик
Напомним, что в равенстве , где , , — некоторые числа, и называются слагаемыми, а — суммой.
Но кроме универсального способа сложения в столбик есть еще несколько способов, которые помогают считать быстрее и удобнее. Речь идет о свойствах сложения.
I. Переместительное свойство сложения. От перестановки слагаемых сумма не меняется.
3+17=17+3
Буквенная запись свойства: a + b = b + a
II. Сочетательное свойство. Чтобы к сумме двух чисел прибавить третье число, нужно к первому слагаемому прибавить сумму второго и третьего слагаемых. Или другими словами, результат сложения трёх и более слагаемых не изменится, если какие-нибудь из слагаемых заменить на их сумму:
(а + b) + c = a + (b + c)
III. Сложение с числом 0
Если к числу прибавить 0, то получится то же самое число.
b + 0 = b
0 + b = b
Пример 1
Упростите выражение 184 + (b + 106)
Решение
Используем переместительное свойство в скобках:
184 + (106 + b), затем сочетательное свойство:
(184 + 106) + b= 290 + b
Ответ: 290 + b
Пример 2
Вычислите: 4 ч 47 мин + 6 ч 21 мин
Решение
1ч= 60 мин.
4 ч 47 мин +6 ч 21 мин = 4 ч + 47 мин +6 ч + 21 мин =
= (4 ч +6 ч) + (47 мин +21 мин) = 10 ч +68 мин = 10 ч + 60 мин + 8 мин=
= 10 ч + 1 ч + 8 мин = 11 ч 8 мин.
Ответ: 11 ч 8 мин.
Упражнение 1
Выполните сложение, выбирая удобный порядок вычислений:
а) (486 + 351) + 514;
б) 2 786 + 871 + 129;
в) 147 + 256 + 353 + 244;
г) (3 681 + 11 388) + (4 319 + 1 612).
Упражнение 2
Упростите выражение:
а) (26 + m) + 34;
б)) 235 + (565 + n);
в) 1 353 + 2 097 + р.
Контрольные вопросы
1. Назовите компоненты сложения?
2. Что означает запись a + b = b + a?
3. Расскажите сочетательное свойство сложения.
4. Что происходит с числом, если к нему прибавляется 0?
Итоги:
1. От перестановки слагаемых сумма не меняется.
2. Результат сложения трёх и более слагаемых не изменится, если какие-нибудь из слагаемых заменить на их сумму.
3. Если к числу прибавить 0, то получится то же самое число.
Упражнение 1
а) (486 + 351) + 514 = (486 + 514) + 351 = 1000 + 351 = 1351;
б) 2786 + (871 + 129) = 2786 + 1000 = 3786;
в) 147 + 256 + 353 + 244 = (147 + 353) + (256 + 244) = 500 + 500 = 1000;
г) (3681 + 11 388) + (4319 + 1612) = (3681 + 4319) + (11 388 + 1612) =
= 8000 + 13 000 = 21 000.
Упражнение 2
а) (26 + m) + 34 = (26 + 34) + m = 60 + m;
б) 235 + (565 + n) = (235 + 565) + n = 800 + n;
в) 1353 + 2097 + р = 3450 + р.



